what two conditions must be met for an object to be in equilibrium what is meant

12 Static Equilibrium and Elasticity

12.1 Conditions for Static Equilibrium

Learning Objectives

By the terminate of this section, yous will be able to:

Identify the concrete conditions of static equilibrium.
Draw a free-body diagram for a rigid body acted on past forces.
Explicate how the weather condition for equilibrium let us to solve statics issues.

We say that a rigid trunk is in equilibrium when both its linear and angular dispatch are null relative to an inertial frame of reference. This means that a body in equilibrium can be moving, just if and so, its linear and angular velocities must exist constant. We say that a rigid body is in static equilibrium when it is at rest in our selected frame of reference. Notice that the stardom between the country of residuum and a state of compatible movement is artificial—that is, an object may be at rest in our selected frame of reference, withal to an observer moving at constant velocity relative to our frame, the same object appears to exist in uniform motion with constant velocity. Considering the motion is relative, what is in static equilibrium to us is in dynamic equilibrium to the moving observer, and vice versa. Since the laws of physics are identical for all inertial reference frames, in an inertial frame of reference, at that place is no distinction between static equilibrium and equilibrium.

According to Newton'south 2d police force of motility, the linear dispatch of a rigid torso is caused by a internet force acting on it, or

$\sum _{k}{\overset{\to }{F}}_{k}=m{\overset{\to }{a}}_{\text{CM}}.$

Here, the sum is of all external forces acting on the torso, where grand is its mass and

${\overset{\to }{a}}_{\text{CM}}$

is the linear dispatch of its center of mass (a concept we discussed in Linear Momentum and Collisions on linear momentum and collisions). In equilibrium, the linear acceleration is null. If we gear up the acceleration to cipher in (Figure), we obtain the following equation:

Kickoff Equilibrium Condition

The starting time equilibrium condition for the static equilibrium of a rigid trunk expresses translational equilibrium:

$\sum _{k}{\overset{\to }{F}}_{k}=\overset{\to }{0}.$

The first equilibrium condition, (Figure), is the equilibrium condition for forces, which we encountered when studying applications of Newton's laws.

This vector equation is equivalent to the following 3 scalar equations for the components of the net strength:

$\sum _{k}{F}_{kx}=0,\quad \sum _{k}{F}_{ky}=0,\quad \sum _{k}{F}_{kz}=0.$

Analogously to (Figure), we can country that the rotational acceleration

$\overset{\to }{\alpha }$

of a rigid body virtually a fixed axis of rotation is caused by the net torque acting on the body, or

$\sum _{k}{\overset{\to }{\tau }}_{k}=I\overset{\to }{\alpha }.$

Hither

$I$

is the rotational inertia of the body in rotation virtually this axis and the summation is over all torques

${\overset{\to }{\tau }}_{k}$

of external forces in (Figure). In equilibrium, the rotational acceleration is zero. Past setting to aught the right-manus side of (Figure), we obtain the second equilibrium condition:

2d Equilibrium Status

The 2nd equilibrium condition for the static equilibrium of a rigid trunk expresses rotational equilibrium:

$\sum _{k}{\overset{\to }{\tau }}_{k}=\overset{\to }{0}.$

The second equilibrium condition, (Effigy), is the equilibrium status for torques that we encountered when we studied rotational dynamics. It is worth noting that this equation for equilibrium is more often than not valid for rotational equilibrium well-nigh any axis of rotation (fixed or otherwise). Once again, this vector equation is equivalent to three scalar equations for the vector components of the net torque:

$\sum _{k}{\tau }_{kx}=0,\quad \sum _{k}{\tau }_{ky}=0,\quad \sum _{k}{\tau }_{kz}=0.$

The second equilibrium condition ways that in equilibrium, in that location is no net external torque to cause rotation about whatever centrality.

The commencement and second equilibrium atmospheric condition are stated in a particular reference frame. The first condition involves simply forces and is therefore independent of the origin of the reference frame. Nonetheless, the second condition involves torque, which is defined equally a cantankerous production,

${\overset{\to }{\tau }}_{k}={\overset{\to }{r}}_{k}\,×\,{\overset{\to }{F}}_{k},$

where the position vector

${\overset{\to }{r}}_{k}$

with respect to the axis of rotation of the indicate where the force is applied enters the equation. Therefore, torque depends on the location of the axis in the reference frame. However, when rotational and translational equilibrium conditions hold simultaneously in one frame of reference, so they likewise hold in whatsoever other inertial frame of reference, and so that the net torque about any axis of rotation is nonetheless zilch. The caption for this is fairly straightforward.

Suppose vector

$\overset{\to }{R}$

is the position of the origin of a new inertial frame of reference

$S\prime$

in the old inertial frame of reference S. From our study of relative movement, we know that in the new frame of reference

$S\prime ,$

the position vector

${{\overset{\to }{r}}^{\prime }}_{k}$

of the point where the forcefulness

${\overset{\to }{F}}_{k}$

is practical is related to

${\overset{\to }{r}}_{k}$

via the equation

${{\overset{\to }{r}}^{\prime }}_{k}={\overset{\to }{r}}_{k}-\overset{\to }{R}.$

At present, we can sum all torques

${{\overset{\to }{\tau }}^{\prime }}_{k}={{\overset{\to }{r}}^{\prime }}_{k}\,×\,{\overset{\to }{F}}_{k}$

of all external forces in a new reference frame,

$S\prime :$

$\sum _{k}{{\overset{\to }{\tau }}^{\prime }}_{k}=\sum _{k}{{\overset{\to }{r}}^{\prime }}_{k}\,×\,{\overset{\to }{F}}_{k}=\sum _{k}({\overset{\to }{r}}_{k}-\overset{\to }{R})\,×\,{\overset{\to }{F}}_{k}=\sum _{k}{\overset{\to }{r}}_{k}\,×\,{\overset{\to }{F}}_{k}-\sum _{k}\overset{\to }{R}\,×\,{\overset{\to }{F}}_{k}=\sum _{k}{\overset{\to }{\tau }}_{k}-\overset{\to }{R}\,×\,\sum _{k}{\overset{\to }{F}}_{k}=\overset{\to }{0}.$

In the last stride in this chain of reasoning, nosotros used the fact that in equilibrium in the quondam frame of reference, S, the start term vanishes considering of (Figure) and the 2nd term vanishes because of (Effigy). Hence, nosotros run into that the net torque in any inertial frame of reference

$S\prime$

is zero, provided that both conditions for equilibrium hold in an inertial frame of reference Southward.

The practical implication of this is that when applying equilibrium weather condition for a rigid body, we are free to cull whatever point equally the origin of the reference frame. Our option of reference frame is dictated past the physical specifics of the problem nosotros are solving. In 1 frame of reference, the mathematical form of the equilibrium conditions may be quite complicated, whereas in another frame, the same conditions may have a simpler mathematical grade that is easy to solve. The origin of a selected frame of reference is called the pivot bespeak .

In the most general case, equilibrium weather are expressed by the half-dozen scalar equations ((Figure) and (Figure)). For planar equilibrium bug with rotation about a fixed axis, which we consider in this affiliate, we can reduce the number of equations to three. The standard procedure is to adopt a frame of reference where the z-axis is the centrality of rotation. With this selection of centrality, the internet torque has simply a z-component, all forces that have non-zero torques lie in the xy-plane, and therefore contributions to the net torque come from simply the x– and y-components of external forces. Thus, for planar problems with the axis of rotation perpendicular to the xy-plane, we have the post-obit three equilibrium conditions for forces and torques:

${F}_{1x}+{F}_{2x}+\text{⋯}+{F}_{Nx}=0$

${F}_{1y}+{F}_{2y}+\text{⋯}+{F}_{Ny}=0$

${\tau }_{1}+{\tau }_{2}+\text{⋯}+{\tau }_{N}=0$

where the summation is over all N external forces acting on the trunk and over their torques. In (Effigy), we simplified the note by dropping the subscript z, but we sympathize here that the summation is over all contributions along the z-centrality, which is the axis of rotation. In (Figure), the z-component of torque

${\overset{\to }{\tau }}_{k}$

from the force

${\overset{\to }{F}}_{k}$

${\tau }_{k}={r}_{k}{F}_{k}\text{sin}\,\theta$

where

${r}_{k}$

is the length of the lever arm of the forcefulness and

${F}_{k}$

is the magnitude of the strength (as you saw in Fixed-Axis Rotation). The angle

$\theta$

is the angle between vectors

${\overset{\to }{r}}_{k}$

and

${\overset{\to }{F}}_{k},$

measuring from vector

${\overset{\to }{r}}_{k}$

to vector

${\overset{\to }{F}}_{k}$

in the counterclockwise direction ((Effigy)). When using (Figure), we often compute the magnitude of torque and assign its sense every bit either positive

$(+)$

or negative

$(-),$

depending on the management of rotation acquired by this torque alone. In (Figure), net torque is the sum of terms, with each term computed from (Effigy), and each term must take the correct sense. Similarly, in (Figure), nosotros assign the

$+$

sign to force components in the

$+$

ten-direction and the

$-$

sign to components in the

$-$

ten-direction. The same rule must exist consistently followed in (Figure), when computing forcefulness components forth the y-centrality.

Figure A is the schematics of the torque of a force that causes counterclockwise rotation around the axis or rotation. Vector tau is aligned with Z axis and has a positive value. Angle theta that is formed by vectors F and r is bigger than zero. Figure B is the schematics of the torque of a force that causes clockwise rotation around the axis or rotation. Vector tau is aligned with Z axis and has a negative value. Angle theta that is formed by vectors F and r is smaller than zero. — **Effigy 12.2** Torque of a force: (a) When the torque of a forcefulness causes counterclockwise rotation about the axis of rotation, we say that its sense is positive, which means the torque vector is parallel to the axis of rotation. (b) When torque of a strength causes clockwise rotation about the axis, we say that its sense is negative, which means the torque vector is antiparallel to the axis of rotation.

View this demonstration to see ii forces act on a rigid square in 2 dimensions. At all times, the static equilibrium weather given past (Figure) through (Figure) are satisfied. You tin can vary magnitudes of the forces and their lever arms and notice the effect these changes have on the foursquare.

In many equilibrium situations, i of the forces acting on the body is its weight. In gratuitous-trunk diagrams, the weight vector is fastened to the centre of gravity of the trunk. For all practical purposes, the center of gravity is identical to the center of mass, as you learned in Linear Momentum and Collisions on linear momentum and collisions. Merely in situations where a body has a large spatial extension so that the gravitational field is nonuniform throughout its book, are the center of gravity and the center of mass located at dissimilar points. In applied situations, however, even objects as big as buildings or prowl ships are located in a uniform gravitational field on Globe's surface, where the acceleration due to gravity has a abiding magnitude of

$g=9.8\,{\text{m/s}}^{2}.$

In these situations, the eye of gravity is identical to the center of mass. Therefore, throughout this chapter, we utilize the center of mass (CM) as the point where the weight vector is attached. Recall that the CM has a special physical meaning: When an external force is applied to a body at exactly its CM, the trunk every bit a whole undergoes translational motion and such a forcefulness does not crusade rotation.

When the CM is located off the centrality of rotation, a net gravitational torque occurs on an object. Gravitational torque is the torque caused past weight. This gravitational torque may rotate the object if at that place is no back up nowadays to balance it. The magnitude of the gravitational torque depends on how far away from the pivot the CM is located. For instance, in the case of a tipping truck ((Effigy)), the pivot is located on the line where the tires brand contact with the route'southward surface. If the CM is located high above the route's surface, the gravitational torque may be large enough to turn the truck over. Passenger cars with a low-lying CM, close to the pavement, are more than resistant to tipping over than are trucks.

Figure A shows an evenly loaded truck with the center of gravity within the area of support. Figure B shows a truck with the center of gravity outside the area of support that is close to turning over. A car in equilibrium is shown next to it for the comparison. Figure C is the schematics that shows the position of the combined center of mass, a combination of load and truck centers of mass, between the two wheels that keep the vehicle stable. Figure D is the schematics that shows the position of the combined center of mass, a combination of load and truck centers of mass, outside the two wheels that make the vehicle unstable and can cause it to tip over. — **Effigy 12.3** The distribution of mass affects the position of the center of mass (CM), where the weight vector
$\overset{\to }{w}$

is fastened. If the center of gravity is within the surface area of support, the truck returns to its initial position subsequently tipping [see the left panel in (b)]. Just if the heart of gravity lies outside the area of support, the truck turns over [see the right panel in (b)]. Both vehicles in (b) are out of equilibrium. Discover that the machine in (a) is in equilibrium: The low location of its centre of gravity makes it hard to tip over.

If you tilt a box so that one edge remains in contact with the tabular array beneath it, then 1 edge of the base of support becomes a pin. As long as the center of gravity of the box remains over the base of support, gravitational torque rotates the box back toward its original position of stable equilibrium. When the centre of gravity moves outside of the base of support, gravitational torque rotates the box in the opposite direction, and the box rolls over. View this demonstration to experiment with stable and unstable positions of a box.

Case

Center of Gravity of a Auto

A passenger car with a 2.v-yard wheelbase has 52% of its weight on the front wheels on level ground, as illustrated in (Effigy). Where is the CM of this car located with respect to the rear axle?

Picture shows a passenger car with a 2.5-m wheelbase that has 52% of its weight on the front wheels and 48% of its weight on the rear wheels on level ground. Distance between the rear axle and the center of mass is x. — **Effigy 12.4** The weight distribution betwixt the axles of a car. Where is the centre of gravity located?

Strategy

We practice not know the weight w of the car. All we know is that when the automobile rests on a level surface, 0.52west pushes downwardly on the surface at contact points of the front wheels and 0.48w pushes down on the surface at contact points of the rear wheels. As well, the contact points are separated from each other by the distance

$d=2.5\,\text{m}.$

At these contact points, the car experiences normal reaction forces with magnitudes

${F}_{\text{F}}=0.52w$

and

${F}_{\text{R}}=0.48w$

on the front and rear axles, respectively. Nosotros also know that the motorcar is an example of a rigid body in equilibrium whose entire weight westward acts at its CM. The CM is located somewhere betwixt the points where the normal reaction forces act, somewhere at a distance 10 from the bespeak where

${F}_{R}$

acts. Our job is to find x. Thus, we identify three forces interim on the body (the automobile), and we can draw a complimentary-body diagram for the extended rigid torso, as shown in (Effigy).

Figure are schematics that show the mass distribution for a passenger car with a wheelbase defined as d. Car has 52% of its weight on the front wheels (labeled as Ff) and 48% on the rear wheels (labeled Fr) and is on level ground. Distance between the rear axle and the center of mass (labeled rR) is x. Distance between the front axle and the center of mass (labeled rF) is d - x. — **Figure 12.v** The free-body diagram for the car clearly indicates forcefulness vectors acting on the automobile and distances to the center of mass (CM). When CM is selected as the pin point, these distances are lever arms of normal reaction forces. Find that vector magnitudes and lever arms do not demand to be fatigued to scale, just all quantities of relevance must be clearly labeled.

We are almost ready to write down equilibrium conditions (Effigy) through (Figure) for the car, but first nosotros must decide on the reference frame. Suppose we choose the 10-axis along the length of the car, the y-axis vertical, and the z-axis perpendicular to this xy-plane. With this choice nosotros only need to write (Effigy) and (Figure) because all the y-components are identically nix. Now we demand to decide on the location of the pivot point. We can choose any point as the location of the axis of rotation (z-axis). Suppose we place the axis of rotation at CM, as indicated in the free-trunk diagram for the auto. At this point, we are ready to write the equilibrium conditions for the car.

Solution

Each equilibrium condition contains only 3 terms considering in that location are

$N=3$

forces acting on the car. The first equilibrium status, (Figure), reads

$+{F}_{\text{F}}-w+{F}_{\text{R}}=0.$

This condition is trivially satisfied considering when nosotros substitute the data, (Effigy) becomes

$+0.52w-w+0.48w=0.$

The second equilibrium condition, (Effigy), reads

${\tau }_{\text{F}}+{\tau }_{w}+{\tau }_{\text{R}}=0$

where

${\tau }_{\text{F}}$

is the torque of strength

${F}_{\text{F}},\,{\tau }_{w}$

is the gravitational torque of force w, and

${\tau }_{\text{R}}$

is the torque of force

${F}_{\text{R}}.$

When the pin is located at CM, the gravitational torque is identically nix because the lever arm of the weight with respect to an axis that passes through CM is zero. The lines of action of both normal reaction forces are perpendicular to their lever artillery, and then in (Effigy), we accept

$|\,\text{sin}\,\theta |=1$

for both forces. From the free-body diagram, nosotros read that torque

${\tau }_{\text{F}}$

causes clockwise rotation nearly the pin at CM, so its sense is negative; and torque

${\tau }_{\text{R}}$

causes counterclockwise rotation near the pivot at CM, so its sense is positive. With this information, we write the second equilibrium condition equally

$\text{−}{r}_{\text{F}}{F}_{\text{F}}+{r}_{\text{R}}{F}_{\text{R}}=0.$

With the help of the free-torso diagram, we identify the force magnitudes

${F}_{\text{R}}=0.48w$

and

${F}_{\text{F}}=0.52w,$

and their corresponding lever arms

${r}_{\text{R}}=x$

and

${r}_{\text{F}}=d-x.$

Nosotros can now write the second equilibrium status, (Figure), explicitly in terms of the unknown distance x:

$-0.52(d-x)w+0.48xw=0.$

Hither the weight westward cancels and we can solve the equation for the unknown position ten of the CM. The reply is

$x=0.52d=0.52(2.5\,\text{m})=1.3\,\text{m}\text{.}$

Solution

Choosing the pivot at the position of the front end axle does non modify the result. The free-torso diagram for this pin location is presented in (Figure). For this choice of pin point, the 2nd equilibrium condition is

$\text{−}{r}_{w}w+{r}_{\text{R}}{F}_{\text{R}}=0.$

When we substitute the quantities indicated in the diagram, we obtain

$\text{−}(d-x)w+0.48dw=0.$

The answer obtained by solving (Figure) is, again,

$x=0.52d=1.3\,\text{m}.$

Figure is the schematics that shows the mass distribution for a passenger car with a wheelbase defined as d. The car has 52% of its weight on its front wheels, now circled and labeled Pivot (Ff) and 48% of its weight on the rear wheels (Fr) on level ground. Distance between the rear axle and the center of mass is x. Distance between the front axle and the center of mass (rw) is d - x. The entire length of the whole axis is labeled with the equation rR=d. — **Effigy 12.6** The equivalent free-torso diagram for the auto; the pivot is clearly indicated.

Significance

This example shows that when solving static equilibrium bug, nosotros are gratis to choose the pivot location. For different choices of the pivot point we have dissimilar sets of equilibrium weather to solve. However, all choices lead to the same solution to the trouble.

Check Your Understanding

Solve (Figure) by choosing the pivot at the location of the rear beam.

[reveal-answer q="fs-id1163713143559″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1163713143559″]

$x=1.3\,\text{m}$

[/hidden-answer]

Check Your Understanding

Explain which one of the post-obit situations satisfies both equilibrium conditions: (a) a tennis ball that does non spin every bit it travels in the air; (b) a pelican that is gliding in the air at a constant velocity at one altitude; or (c) a crankshaft in the engine of a parked automobile.

[reveal-answer q="fs-id1163709667984″]Show Solution[/reveal-answer]

[hidden-reply a="fs-id1163709667984″]

(b), (c)

[/hidden-reply]

A special case of static equilibrium occurs when all external forces on an object act at or along the axis of rotation or when the spatial extension of the object tin be overlooked. In such a case, the object can be effectively treated like a point mass. In this special case, we need not worry about the 2d equilibrium status, (Figure), because all torques are identically goose egg and the first equilibrium status (for forces) is the only condition to be satisfied. The free-body diagram and problem-solving strategy for this special case were outlined in Newton's Laws of Motion and Applications of Newton'south Laws. You will come across a typical equilibrium situation involving just the first equilibrium condition in the next example.

View this demonstration to see 3 weights that are connected by strings over pulleys and tied together in a knot. You can experiment with the weights to see how they affect the equilibrium position of the knot and, at the aforementioned time, see the vector-diagram representation of the commencement equilibrium condition at piece of work.

Example

A Breaking Tension

A small-scale pan of mass 42.0 g is supported by 2 strings, as shown in (Effigy). The maximum tension that the string tin can support is ii.fourscore N. Mass is added gradually to the pan until one of the strings snaps. Which string is information technology? How much mass must be added for this to occur?

Figure shows small pan of mass supported by two strings intersecting at a 90 degree angle. The length of one string is 5 centimeters, the length of another string is 10 centimeters. — **Effigy 12.7** Mass is added gradually to the pan until one of the strings snaps.

Strategy

This mechanical system consisting of strings, masses, and the pan is in static equilibrium. Specifically, the knot that ties the strings to the pan is in static equilibrium. The knot can be treated as a point; therefore, we demand merely the first equilibrium status. The three forces pulling at the knot are the tension

${\overset{\to }{T}}_{1}$

in the 5.0-cm string, the tension

${\overset{\to }{T}}_{2}$

in the 10.0-cm string, and the weight

$\overset{\to }{w}$

of the pan belongings the masses. We adopt a rectangular coordinate system with the y-axis pointing contrary to the direction of gravity and draw the free-body diagram for the knot (see (Effigy)). To find the tension components, we must identify the management angles

${\alpha }_{1}$

and

${\alpha }_{2}$

that the strings brand with the horizontal direction that is the x-axis. As you can run into in (Effigy), the strings make two sides of a right triangle. Nosotros tin use the Pythagorean theorem to solve this triangle, shown in (Figure), and observe the sine and cosine of the angles

${\alpha }_{1}$

and

${\alpha }_{2}.$

Then we can resolve the tensions into their rectangular components, substitute in the kickoff condition for equilibrium ((Figure) and (Figure)), and solve for the tensions in the strings. The cord with a greater tension will pause first.

Top figure shows the distribution of forces for the knot that ties the strings to the pan. T1 and T2 forces are pulling at the knot upward. Weight, a sum of M and m multiplied by g is pulling the knot downward. Projections of T1 and T2 at the x and y axes are shown. Bottom figure shows the representation of the knot that ties the strings to the pan as a right triangle. It has legs of the length a and 2a with a being equal 5 centimeters. Hypotenuse is a square root of five. Angle alpha 1 is formed by shorter leg and hypotenuse. Angle alpha 2 is formed by the longer leg and hypotenuse. Cosine of angle alpha 1 is equal to sine of angle alpha 2 and is equal to one divided by square root of five. Cosine of angle alpha 2 is equal to sine of angle alpha 1 and is equal to two divided by square root of five. — **Figure 12.8** Complimentary-torso diagram for the knot in (Effigy).

Solution

The weight w pulling on the knot is due to the mass K of the pan and mass m added to the pan, or

$w=(M+m)g.$

With the aid of the gratis-body diagram in (Figure), we can set up the equilibrium conditions for the knot:

$\begin{array}{ccccc}\text{in the}\,x\text{-direction,}\hfill & & \hfill \text{−}{T}_{1x}+{T}_{2x}& =\hfill & 0\hfill \\ \text{in the}\,y\text{-direction,}\hfill & & \hfill \text{+}{T}_{1y}+{T}_{2y}-w& =\hfill & 0.\hfill \end{array}$

From the gratis-body diagram, the magnitudes of components in these equations are

$\begin{array}{ccc}{T}_{1x}={T}_{1}\text{cos}\,{\alpha }_{1}={T}_{1}\text{/}\sqrt{5},\hfill & & {T}_{1y}={T}_{1}\text{sin}\,{\alpha }_{1}=2{T}_{1}\text{/}\sqrt{5}\hfill \\ {T}_{2x}={T}_{2}\text{cos}\,{\alpha }_{2}=2{T}_{2}\text{/}\sqrt{5},\hfill & & {T}_{2y}={T}_{2}\text{sin}\,{\alpha }_{2}={T}_{2}\text{/}\sqrt{5}.\hfill \end{array}$

We substitute these components into the equilibrium weather and simplify. We then obtain two equilibrium equations for the tensions:

$\begin{array}{ccccc}\text{in}\,x\text{-direction,}\hfill & & \hfill {T}_{1}& =\hfill & 2{T}_{2}\hfill \\ \text{in}\,y\text{-direction,}\hfill & & \hfill \frac{2{T}_{1}}{\sqrt{5}}+\frac{{T}_{2}}{\sqrt{5}}& =\hfill & (M+m)g.\hfill \end{array}$

The equilibrium equation for the x-direction tells us that the tension

${T}_{1}$

in the 5.0-cm string is twice the tension

${T}_{2}$

in the ten.0-cm string. Therefore, the shorter cord will snap. When nosotros apply the commencement equation to eliminate

${T}_{2}$

from the 2nd equation, we obtain the relation between the mass

$m$

on the pan and the tension

${T}_{1}$

in the shorter string:

$2.5{T}_{1}\text{/}\sqrt{5}=(M+m)g.$

The cord breaks when the tension reaches the critical value of

${T}_{1}=2.80\,\text{N}.$

The preceding equation can be solved for the disquisitional mass yard that breaks the string:

$m=\frac{2.5}{\sqrt{5}}\,\frac{{T}_{1}}{g}-M=\frac{2.5}{\sqrt{5}}\,\frac{2.80\,\text{N}}{9.8\,\text{m}\text{/}{\text{s}}^{2}}-0.042\,\text{kg}=0.277\,\text{kg}=277.0\,\text{g.}$

Significance

Suppose that the mechanical arrangement considered in this example is attached to a ceiling within an elevator going up. Every bit long as the elevator moves upward at a constant speed, the result stays the same because the weight

$w$

does not change. If the elevator moves upwards with acceleration, the critical mass is smaller because the weight of

$M+m$

becomes larger by an apparent weight due to the acceleration of the elevator. Notwithstanding, in all cases the shorter cord breaks first.

Summary

A body is in equilibrium when it remains either in uniform motion (both translational and rotational) or at residuum. When a torso in a selected inertial frame of reference neither rotates nor moves in translational move, we say the body is in static equilibrium in this frame of reference.
Conditions for equilibrium require that the sum of all external forces interim on the body is zero (showtime condition of equilibrium), and the sum of all external torques from external forces is zero (second status of equilibrium). These two atmospheric condition must be simultaneously satisfied in equilibrium. If ane of them is not satisfied, the body is not in equilibrium.
The gratuitous-body diagram for a body is a useful tool that allows u.s. to count correctly all contributions from all external forces and torques acting on the trunk. Free-trunk diagrams for the equilibrium of an extended rigid torso must point a pivot point and lever arms of acting forces with respect to the pivot.

Conceptual Questions

What tin you say about the velocity of a moving body that is in dynamic equilibrium?

[reveal-answer q="fs-id1163713268541″]Show Solution[/reveal-reply]

[subconscious-respond a="fs-id1163713268541″]

constant

[/hidden-answer]

Under what conditions can a rotating torso be in equilibrium? Requite an case.

What three factors touch the torque created by a force relative to a specific pivot betoken?

[reveal-answer q="fs-id1163713358733″]Testify Solution[/reveal-respond]

[hidden-answer a="fs-id1163713358733″]

magnitude and direction of the force, and its lever arm

[/hidden-answer]

Mechanics sometimes put a length of pipage over the handle of a wrench when trying to remove a very tight bolt. How does this help?

For the next four bug, evaluate the statement equally either true or false and explain your answer.

If at that place is just i external force (or torque) acting on an object, it cannot be in equilibrium.

[reveal-respond q="fs-id1163713282665″]Testify Solution[/reveal-reply]

[hidden-answer a="fs-id1163713282665″]

True, as the sum of forces cannot be nada in this case unless the force itself is zero.

[/hidden-respond]

If an object is in equilibrium there must exist an even number of forces acting on it.

If an odd number of forces human action on an object, the object cannot be in equilibrium.

[reveal-reply q="fs-id1163709692362″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1163709692362″]

Simulated, provided forces add to zero as vectors then equilibrium can be achieved.

[/hidden-answer]

A body moving in a circle with a abiding speed is in rotational equilibrium.

What purpose is served by a long and flexible pole carried by wire-walkers?

[reveal-answer q="fs-id1163713272740″]Evidence Solution[/reveal-answer]

[subconscious-answer a="fs-id1163713272740″]

Information technology helps a wire-walker to maintain equilibrium.

[/hidden-answer]

Problems

When tightening a bolt, you push perpendicularly on a wrench with a forcefulness of 165 Due north at a distance of 0.140 chiliad from the center of the bolt. How much torque are yous exerting relative to the center of the bolt?

When opening a door, you push button on it perpendicularly with a force of 55.0 N at a distance of 0.850 m from the hinges. What torque are you exerting relative to the hinges?

[reveal-reply q="fs-id1163713470139″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1163713470139″]

$46.8\,\text{N}·\text{m}$

[/subconscious-answer]

Find the magnitude of the tension in each supporting cable shown below. In each case, the weight of the suspended body is 100.0 North and the masses of the cables are negligible.

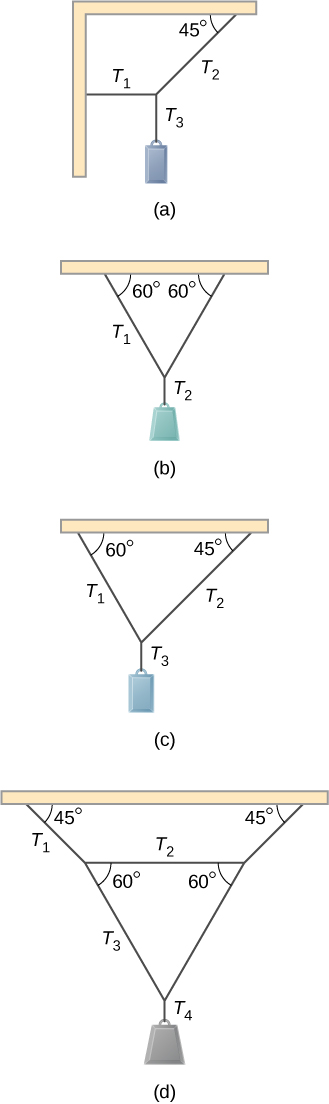
What forcefulness must be practical at point P to keep the structure shown in equilibrium? The weight of the structure is negligible.

Figure shows the distribution of forces applied to point P. Force of 2000 N, two meters to the left of the point P, moves it downwards. Force of 4000 N, two meters to the right and one meter above of the point P, moves it to the right.

[reveal-answer q="264812″]Show Answer[/reveal-answer]
[hidden-answer a="264812″]153.4°[/hidden-answer]

Is it possible to employ a forcefulness at P to continue in equilibrium the structure shown? The weight of the structure is negligible.

Figure shows the distribution of forces applied to point P. Force of 2000 N, two meters to the left of the point P, moves it downwards. Force of 3000 N, two meters to the right of the point P, moves it upwards. Force of 5000 N, two meters to the right and one meter above of the point P, moves it to the right.

Two children push button on opposite sides of a door during play. Both push horizontally and perpendicular to the door. 1 child pushes with a force of 17.five North at a distance of 0.600 m from the hinges, and the second child pushes at a distance of 0.450 m. What forcefulness must the second kid exert to proceed the door from moving? Presume friction is negligible.

[reveal-answer q="fs-id1163713183876″]Prove Solution[/reveal-answer]

[hidden-respond a="fs-id1163713183876″]

23.3 Northward

[/hidden-answer]

A small 1000-kg SUV has a bicycle base of 3.0 thousand. If lx% if its weight rests on the front wheels, how far behind the forepart wheels is the wagon'south center of mass?

The uniform seesaw is counterbalanced at its eye of mass, as seen below. The smaller boy on the right has a mass of 40.0 kg. What is the mass of his friend?

Figure is a schematic drawing of two boys on the seesaw. One boy sits two meters from the edge of the seesaw and two meters from the center. Another boys sits at the opposite edge of the seesaw, four meters from the center.

[reveal-answer q="920895″]Show Answer[/reveal-answer]
[hidden-answer a="920895″]80.0 kg[/subconscious-answer]

Glossary

eye of gravity: signal where the weight vector is attached

equilibrium: body is in equilibrium when its linear and angular accelerations are both zero relative to an inertial frame of reference

first equilibrium status: expresses translational equilibrium; all external forces acting on the trunk balance out and their vector sum is zero

gravitational torque: torque on the body caused past its weight; information technology occurs when the center of gravity of the body is non located on the axis of rotation

second equilibrium condition: expresses rotational equilibrium; all torques due to external forces acting on the trunk remainder out and their vector sum is goose egg

static equilibrium: body is in static equilibrium when it is at rest in our selected inertial frame of reference

smithcarroo.blogspot.com

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/12-1-conditions-for-static-equilibrium/

what two conditions must be met for an object to be in equilibrium what is meant

12.1 Conditions for Static Equilibrium

Learning Objectives

Kickoff Equilibrium Condition

2d Equilibrium Status

Case

Center of Gravity of a Auto

Strategy

Solution

Solution

Significance

Check Your Understanding

Check Your Understanding

Example

A Breaking Tension

Strategy

Solution

Significance

Summary

Conceptual Questions

Problems

Glossary

0 Response to "what two conditions must be met for an object to be in equilibrium what is meant"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel